この記事はある高校生に送った『誕生日プレゼント』。
そのときの題名は『数学の面白さ~「データ分析」を通して~』。
内容を少し修正して記事を公開しました。高校1年生で習う「データ分析」の中の「相関分析」がメインで出てきます。

統計なんて意味ない!難しい!やりたくなーい!

という人に読んでもらいたい記事です。
なぜ統計(数Ⅰの『データ分析』)は面白くないのか?
この小見出し「なぜ数Ⅰの『データ分析』は面白くないのか?」を英語にすると、
“Why is Data analysis of MathⅠ kimoi?”
なぜこんなにも『データ分析』がキモいのか、まずそこから論じてみる必要がある。(今の高校生は「難しい」の5段階上が「キモイ」だそうだ)
私が『データ分析』を習得したのは社会人に入ってからである。高校生で習った記憶は全く無い(覚えてない)。会社のセミナーでQC検定(品質管理検定)という資格を取るために『データ分析』のセミナーを受講した。
高校の数Ⅰの教科書に載っているのを知って驚いたが、これは統計学という分野でもある。受講したセミナーはハッキリ言って眠かった。眠すぎて死にかけた。まぶたの上に数字がのしかかって不可抗力に押しつぶされた(≒寝た)。

図1.居眠りの図
なぜこんなにも眠いのか?もうセミナー聞かなくていいや。原因を分析するという名目でセミナー講師の悪口をノートに書き綴った。
だって、
- 数式むずい!
- Sxyとか、Vとか、σとか、うちらが知っている前提で話さんでよ!
- 黒板に向かって説明すんじゃねぇ!
- 検定とか回帰とか日本語じゃねーだろ!
- 誰もわかってないのに次の話に進まないで!
挙げればきりがないが、一番眠くなる原因は
という結論に至った。
複雑な式を一生懸命計算して、何かいいことあるの?ただの数字遊びじゃないの?そんな思いで、セミナー講師に眠さの次は殺意むき出しで聞いていた。(図2)

図2.セミナーを聞いている私の表情
たしかに統計(数Ⅰの『データ分析』)を習うだけでは、ただの包丁とぎである。
「包丁を一生懸命研ぎなさい。だけど何にも使いません!」
なんて言われたら、その人を包丁で刺したくなるわけだ。(図3)

図3.せっかく研いだのに使わないんだ、へぇー
だから『データ分析』がこんなにも役に立つのだと知ったとき、目が輝いた。
(週1の授業が3ヶ月くらいつづくセミナーで、1ヶ月以上過ぎてからその話があった)先にそれを言えよ!と、セミナー講師をまた刺したくなった。(図4)

図4.それ、一番最初に言おうね
よって『データ分析』はどんな意味があるのか?どんな役に立つのか?について2つ事例を紹介する。初めて読む人でもわかるようになるべく平易に記述したので良かったら読んで欲しい。
事例1:統計(データ分析)で未来を予測する~コンサートの入場者数~
推理の話。
『名探偵コナン』は1994年に開始、今年で30周年を迎える。
初期のコナンは特に耳がデカかった。
-300x292.png)
↑初期の頃
-300x250.png)
↑最近の表紙
図5.コナンの30年前と今
(この目的でのイラストの利用はプライバシー権、パブリシティ権侵害には当たらないと考えていますが、指摘があった場合は削除します)
「体は子供!頭脳は大人!その名も名探偵コナン!」の名台詞が、
- 体10才+30年=40才
- 頭18才+30年=48才
になるから、
「体はオジサン!頭脳もオジサン!その名も名探偵コナン!」になってしまう。
そんな話はどうでもいいとして、話の中で殺人事件現場に遭遇したとき、まず毛利小五郎が登場するのが鉄板である。そして、わけのわからない理由をつけて犯人を名指しする。
この時点で「あ、この人は犯人じゃないな」と推理することが出来る。
私が出来る推理はここまで。後はお手上げである。そしてひょっこり小五郎についてきたコナン君が、
「あれれ~?おかしいぞ~」と言いながら、証拠品を持ち去ったり大人が気づかないように場を荒らしたりして、わずかな手がかりから次々と推理を繰り出し、犯人をぴたりと言い当てる。
一般人には見えていないものが、コナン君には見えているのである。
統計(データ分析)もそれに近いものがある。数字の羅列。それは一見ただの数字にしか見えない。
しかし統計学を駆使すると、数字が語りかけてくるのである。見えないものが見えてくる。
そして数字との会話の結果、この先どうしたらいいのか、自分の未来の行動を判断することができる場合がある。

2023年、ユニット名『カーブス残金』は紅白デビューを果たし、翌年の2024年はすでに全国ツアーを展開している。
そのときの来場人数ともろもろのデータを表にしたものがこれである。(表1)
ユニットを管理しているマネージャーは金野茂(かねのも)卯邪(うじゃ)という。
金野茂がコンサートの場所、日時、金額などを決め『カーブス残金』がコンサートで歌う、というわけである。
ユニットリーダーの名前は、”おとは”。超アグレッシブ、歌うの大好き、でも数学あまり好きじゃない高校生。
表1.全国ツアーの入場者数

表1の説明を簡単にする。
- 日付 ・・1か月に1回のペースで全国を回りコンサートを行っている
- 入場者数 ・・なかなかの人数である(武道館コンサートはMax14500人)
- 曲の数 ・・1回のコンサートで歌う曲の数
- 天気 ・・天気のいい日(晴れ)を3点、天気の悪い日(雨)を1点と数値化
- 開催都市人口・・そう、まだ1桁万人なので、大都市に行ってはいない
- チケットの値段・・金野茂が勝手に決めている。おとは「安い時と高い時の差がありすぎじゃないかしら?」
この表1を漠然と眺めているだけでは
おとは「はあ、こんなもんかしらん?」
であるが、ここで相関分析を使うと面白いことがわかる。
たとえば、入場者数をyとし、曲の数をxとしてみる。どんなグラフになるか?(図6)
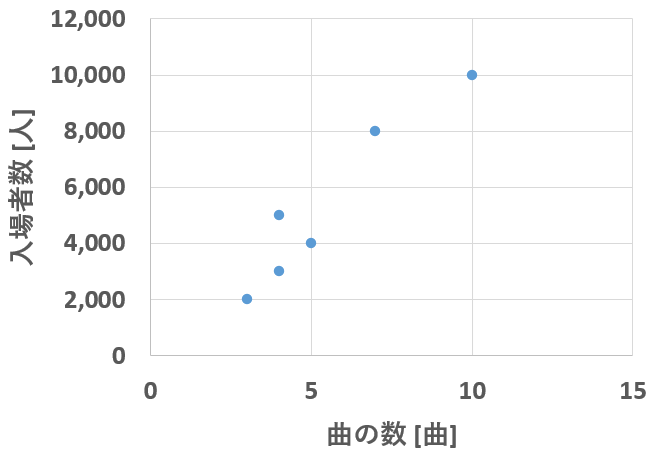
図6.曲の数と入場者数の関係
お?これは右肩上がりだから正の相関がありそうだ。相関係数はいくつだろ?
ここで計算が出てくるとげっそりする。めんどい。。
いやいや、大人はExcel使いますから。計算式なんて忘れたもんねー。
やり方は次の通り。
- Excelの「データ分析」→「相関」(図7)
- 範囲を選択してOKボタン押す(図8)
たったこれだけ。
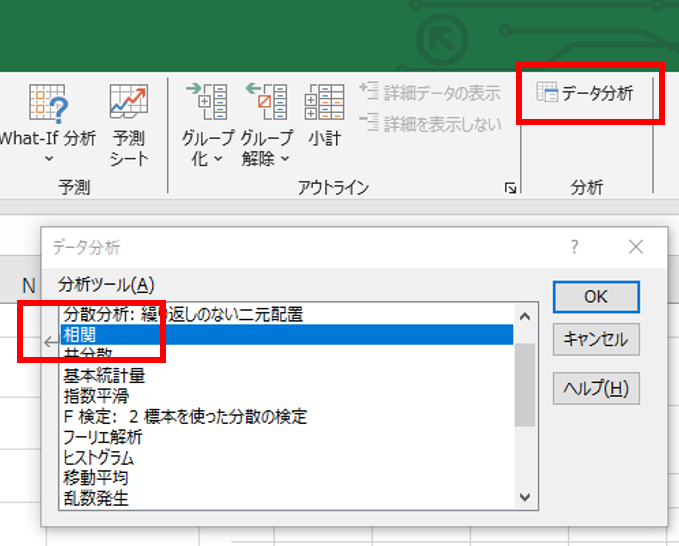
図7.「データ分析」→「相関」を選択
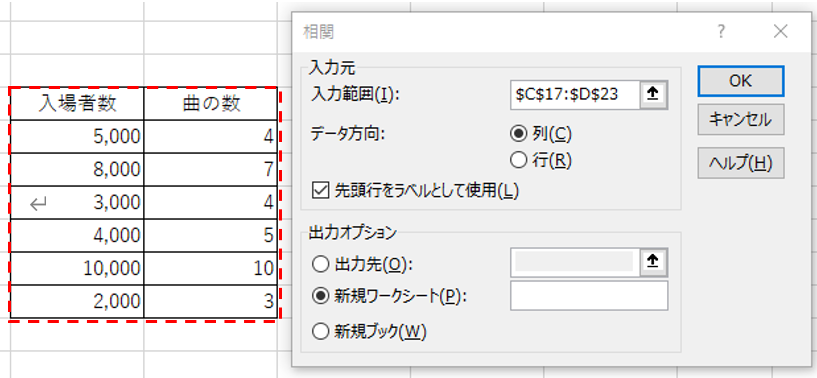
図8.範囲を選択してOKボタン押す
計算すると相関係数R=0.95となった。(表2)
表2.相関係数(入場者数と曲の数の相関)
| 入場者数 | 曲の数 | |
| 入場者数 | 1 | |
| 曲の数 | 0.954 | 1 |
おとは「確かに曲数が多いと入場者数増えるのはわかるよね。」
おとは「7月開催のコンサートは3曲で終了なんてありえへん計画立てとる。そりゃ最低記録(2000人)更新しますわな。」
おとは「他にもデータがいっぱいある。どうやって分析したらええのやろ? xとyをいろいろな組み合わせでやってみたらどうかな?」
これが相関分析である。(表3)
表3.相関分析結果
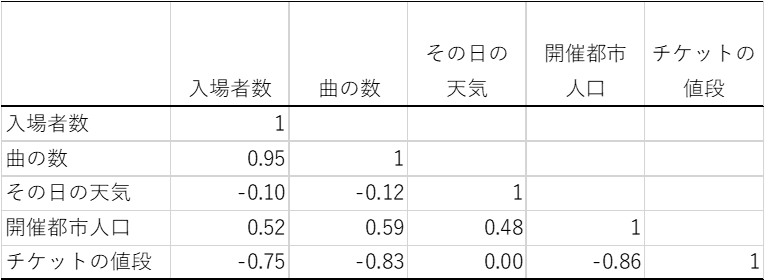
いくつか見てみましょ。
曲の数と入場者数(r=0.95)
「正の相関だね~」ってさっきやった。ここまでだと全くオモロクない。この後が大事。
「正の相関だね~、だから来月のコンサートは曲数を増やせば入場者数は増加しそうだ」
「正の相関だね~」はただの分析結果。これだけだと「へぇ~(だから何?)」となってしまう。
「だから」の接続語以降は、その分析結果に基づいて私はこう行動する、こう判断するということを書いている。
ここがめちゃくちゃ大事。分析した結果から「未来私はこうしたい!」につながって初めて分析に意味が出てくる。
他の相関係数も見てみる。
入場者数とその日の天気(r=-0.10)
おとは「相関係数ほぼ0だから天気はあまり関係ないみたい。屋内だしね。」
入場者数とチケットの値段(r=-0.75)
おとは「負の相関だ。値段が高いとあまり人が集まらない。やっぱりお金は大事ね。」
曲の数と開催都市人口(r=0.59)
おとは「金野茂マネージャー、開催都市人口多いほど曲数を多くぶっこんでる。まったくお金のことしか考えてないんだから。」
曲数とチケットの値段(r=-0.83)
おとは「曲数が多いとチケットの値段が安くなるなんて金野茂マネージャー、アホやん。逆やろ!」
天気と開催都市人口(r=0.48)
おとは「これは絶対たまたまや。いくらマネージャーでも天気はコントロールできないから、もっとコンサート回数を増やしていくとR=0に近づいていくかも?」
そして”おとは”はあることに気づいてしまった・・。
・・・
次のコンサートの打ち合わせ時、『カーブス残金』のリーダー”おとは”は、金野茂卯邪へ一言物申す。
おとは「マネージャー、来月のコンサートもっと人増やしたいんなら、曲数を増やせばいけると思います。だって曲の数と入場者数の相関係数は0.95やから」
金野茂「そうなんか!じゃ曲数増やそ!(儲かるで~!)」
おとは「あと大都市ほど曲数多くぶっこむの止めてくれます?少ない都市でもそれなりに曲入れてみんなに満足してもらいたい」
金野茂「あ。まぁそうやなー・・」
おとは「それと曲数が多いとチケットの値段が安くなるの逆やちゃいます?もう少し考えてください!」
金野茂「お、おう・・(なんか圧が・・)」
おとは「で、最後に。これはどういうことですやろ?」
バン!
”おとは”は金野茂マネージャーから受け取った表に、「売上」「設備運営費用」「カーブス残金お給料」を付け加えた表を突き出した。(表4)
表4.全国ツアーの入場者数+お金

金野茂「ギク!」
おとは「設備運営費用は1回50万円、うちらのお給料は1回50万円。差し引いた残りのお金の1億円はどこいったんやろな~。あれれ~おかしいぞ~?」
金野茂「いや、それは寄付につこうてまんがな・・」
おとは「自分の財布に寄付してどうするんや!!正直さらしいや!この桜吹雪が目に入らんか!」
金野茂「ひぃぃ~!すんませぇ~ん!」
ボコっ!ぽカッ!・・・
金野茂「ぎゃー!」

図9.しばらくお待ち下さい
”おとは”のデータ分析によって金野茂卯邪の悪事は暴かれ、『カーブス残金』の平和は守られた。その後コンサートは適正価格で行われ、全国ツアーは大成功で幕を閉じた。金野茂卯邪も反省し、今は世のため人のために働いているという。

~Fin~
データは語る。とても顕著な事例だ。
事例2:「その水を飲むな!」統計学者と医者の話
セミナー講師から教えてもらった「統計(データ分析)はすごいんだ!」と私が統計大嫌い→大好きに変わって感動した話。
これは実際に中世?のヨーロッパで実際にあったことらしい。どこの国で誰が?を忘れてしまったのが残念でならない。
・・・・
とある町の西と東に川が流れていた。西側の川はA川、東側の川はB川である。(図10)

図10.とある町に流れる川(西側:A川、東側:B川)
住民はこの2つの川の間で、穏やかに暮らしていた。
ところがあるとき、人がバタバタと倒れて死んでいった。
昔でいえばペスト。ペストは世界的大流行が複数回起こっている。14世紀に起きた大流行では、世界人口4億5000万人のうち、1億人が亡くなったと推計されている。
直近ではコロナ。2020年~2022年の間で世界では552万人が亡くなった。
この町でもたくさんの死者が出た。毎日死体が焼かれる。感染症の場合はほっておくと、更に拡大してしまう。医者も学者も昼夜通して調査するが、さっぱり原因かわからない。

時間がたてばたつほど、死体の山が積みあがっていく。
悲惨な状況が拡大する中、ある統計学者が亡くなった人のデータを並べ整理していた。
亡くなる時の症状はみんな同じだから、感染症が疑わしい。しかし、年齢は関係なし、性別も関係ないし、特定の職業に限ったことでもない。
ところが1点気づいたことがあった。
住所である。
統計学者「なぜ亡くなる人はみな町の東側の人ばかりなのだろう?」
亡くなった人の住所をプロットするとこのようになった。(図11)

図11.亡くなった人の分布(オレンジの丸)
そして、統計学者はこのデータからあることに気づいた。
統計学者「水か!」
東側の住民はライフラインとしてB川の水を利用している。反対に西側の人はA川の水を生活に使用している。もし空気感染や人同士の接触感染ならこのような分布には決してならない。
すぐに統計学者は対策会議へ赴き、こう発言した。
統計学者「死亡者の分布は東のB川沿岸に集中している。これだけ大量の死者がでるのはライフラインである水が関係している可能性が非常に高い。すぐにB川の水を飲むのを止めさせてくれ!」
医者1「確かに死者は東側に分布しているが、まだ原因がわからない。正しい原因を見つけて対策を打たなければ」
医者2「すぐに東の川の水質検査の準備をしよう」
統計学者「バカなことを言うな!原因を知ることも大事だが、最優先すべきは一日も早く増え続ける死者を減らし、命を救うことだ!」
あまりの剣幕に押されて、医者たちが言うとおりにしたところ、死亡者数はその日から大幅減少した。
後日調査したところ、上流の工場から有害物質が流れていたことが判明した。当初予想していた感染症ではなく、水質汚染が原因で多くの死者を出していたことが分かった。
原因を知って対策を打つことは当然大事であり、一番の正攻法である。正しい原因を知ってのみ正しい対策が打てる。
しかし、統計学の立場から言うと、原因がわからなくても対策を打つことが出来る場合がある。上の例でいえば、原因を知るのは人を救うための手段。目的は1日も早く命を救うこと。原因がわからなくても対策が打てるならば、すぐに行動に移した方がいいではないか、という立場をとったわけである。
統計学は確かに確率で論じるから外れることもある。しかし、3σ外の異常値を検出したら「99.7%の確率で黒!」とわかるのだから、行動に移さない手はないわけである。
私はこの話を聞いて、セミナー講師に殺意を抱いた。
「もっと早く言ってくれたら、セミナー受講真剣に聞いたのに!!」

図12.(図4の再掲)一番最初に言おうね
まあ私が悪いんだけどね。そのあとはちゃんと聞いた。資格は取るまではいかなかったけど、仕事で役立てられるまでのレベルには到達できた。だってやる気爆上がりだもの。
似たような話は1853年から始まったクリミア戦争でもあったようだ。そこで活躍したナイチンゲールは看護師として有名だが、実は医療統計学の母とも言われている。
クリミア戦争で負傷兵の悲惨な状況を知り、事態を重く見たナイチンゲールは最前線へ赴いた。
通常戦争で傷ついた兵の手当と聞くと、銃弾に打たれたり、ケガをした兵士が多数で亡くなっているということはだれも疑わない。
しかし、ナイチンゲールは現場の状況、データなどから病院内を衛生的に保つことを徹底的に行った。その結果、ナイチンゲール着任直後の死亡率42%が2か月後には15%、さらに次の月には5%にまで低下したのである。
病院での死者は、大多数が傷ではなく、病院内の不衛生によるものだったと後に推測された。このことからナイチンゲールをクリミアの天使、白衣の天使と呼ばれるようになった。
これは、データを分析することで先入観に惑うことなく正しい原因を特定できた例である。ここでも統計が役に立っている。
「統計の意味を物語でわかりやすく解説!」のまとめ
この記事では、
- なぜ統計(数Ⅰの『データ分析』)は面白くないのか?
- 事例1:統計(データ分析)で未来を予測する~コンサートの入場者数~
- 事例2:「その水を飲むな!」統計学者と医者の話
について紹介しました。
目の前の牛乳ビンは涙であふれたでしょうか?(笑)
学校の数学は「やっても意味がない」。どうしてもそう思ってしまいます。
なぜかというと、役立った例を知らないから。先生も教えてくれないから。
役立つということを知ったとき、私はがぜん勉強に力が入りました。
この記事を読んで、少しでも数学に前向きになってくれたなら幸いです。
今は教えてもらうだけでなく、自分で眼の前にある”それ”の意味を自分で考えるようになりましたよ。








コメント