「最大公約数、最小公倍数ってなんだっけ?習ったけど忘れちゃった!」という小学校5~6年生向けの記事です。
この記事では、最大公約数と最小公倍数の言葉の意味をまず解説し、その後に求め方・計算の方法を説明しています。
私は家庭教師などをしていて、子どもに勉強を教えることが多いので、教えるポイントはしっかりとおさえています。
この記事を読むと最大公約数、最小公倍数の言葉の意味、求め方、日常生活でどんな役に立つか?がわかります。難しいことは抜きにして、楽しく学んでいきましょう。
最大公約数、最小公倍数とは?~言葉の意味と求め方~
まず、「最大公約数」と「最小公倍数」という2つの言葉。

どっちがどっちかわからーん!
5つの漢字のうち3つ同じなので、とてもよく似ています。
また、私が子供のころ感じたのは、
- 最大公約数は、「約数(数がちっちゃくなる)」なのに、なぜ「最大」ってつくの?
- 最小公倍数は、「倍数(数が倍、倍、倍)」なのに、なぜ「最小」ってつくの?
でした。
同じ疑問をもっているお子さんもいるかもしれないので、そのあたりもふまえて見ていきましょう。
最大公約数とは?
最大公約数という言葉を分解すると、「最大・公・約数」です。
モンキー・D・ルフィ風に言うと、「いちばんでっけー(最大)、みんながもってる(公)、約数だぜ!」
ということです。

約数の中でも特別な約数のことをいいます。

まず約数とはなにか?おさらいしましょう!
約数とは、ある数が整数で割り切れればその整数はある数の約数です。

まじわからん・・。
例を出したほうが早いですね。
6を例に取ると、ある数6は2という整数で割り切れる。だから2という整数は6の約数です。
6の約数は1、2、3、6で全部。全部で4個あります。6自身も1も約数です。
たまに6の約数は何個ですか?という問題があって、1ってどうだったっけ?とわからなくなる子もいるので、覚えておいてください。
例の2つ目。49の約数は1、7、49です。
例の3つ目。48の約数は、1、2、3、4、6、8、12、16、24、48です。
割り切れる数が多いほど、約数は増えていきます。
これで約数は完ぺき!

次は公約数です。
「公」は公民館とか公共施設という言葉の中に出てきます。
みんなが共通して使える場所だから、公民館、公共施設と言われます。
よって公約数とは、数字が2つ以上あってそれらに共通の約数という意味です。
たとえば、「6と9の公約数は?」という問題があったら「6と9の共通の約数は?」という質問と同じです。
ゲームでタイムラグが発生して画面がカクカクして動きが鈍いことを「ラグい」っていうのと同じ。短い言葉で表現しています。
- 6の約数:1、2、3、6
- 9の約数:1、3、9
共通な約数は1と3なので、6と9の公約数は1、3です。
次の問題。
12と54の公約数は?
- 12の約数:1、2、3、4、6、12
- 54の約数:1、2、3、6、9、18、27、54
よって公約数は1、2、3、6です。これで公約数も完ぺきです。
さて、ようやく最大公約数の出番が来ました。最大公約数は、公約数の中で最大、一番大きなものです。
先程の「12と54の最大公約数は?」という問題だったら、公約数は1、2、3、6なので、この中で一番大きな6が最大公約数です。
ここまでの説明で、『最大公約数は、「約数(数がちっちゃくなる)」なのに「最大」ってつくの?』の疑問もわかりましたね。
ある数の約数は、ある数よりも大きくなることは絶対にありません。6の約数が7とか12とかにはなりません。同じか小さくなります。「最大」とついているのは、その約数の中で一番大きいものという意味です。
比べる範囲が限定されていることをよく理解していなかったことからおきた疑問でした。
たとえば、小学生の中で一番足が速い子を「最速小学生」と名付けたとします。

それは小学生の中で比較しているということ、箱根駅伝に出るような大学生には勝てません。
(大人と表現しなかったのは、負ける大人がたくさんいるから。小学生、本当に走る(逃げ回るの)の速い・・)
最大公約数はもっと簡単な求め方もありますが、私は約数を全部書き出す方がいいかな?と思います。
最大公約数を求める問題で、小学校で出てくる数字は1ケタ~2ケタくらいです。100より大きい数字はまず出てきません。
それに約数を書き出すと数字の特徴がわかってきます。
48や54や72はたくさん約数がある。反対に66、83、91はそんなに約数はありません。
数字見て約数が多そうだ(割り切れる数が多そうだ)、少なそうだ、が直感的にわかると後々の算数・数学の計算が楽になってきます。
最小公倍数とは?
次に最小公倍数の説明です。
これも「最小・公・倍数」です。一番小さい、共通の、倍数という意味です。
まず倍数について。
例えば6ならば、
6の倍数:6、12、18、24・・・
約数の数は限られていますが、倍数は無限にあります。
倍数について屁理屈を言う子もいます。

「9も6の倍数だよ!だって6に1.5かければ9になるもーん!
たしかに6×1.5=9なのですが、倍数の定義(ルール)は、かける数は整数でなければなりません。なので1倍、2倍、3倍・・・です。
「1.5倍かけてもいい!」というのはドッジボールで言えば、線をはみ出して逃げているのと同じです。ルールを無視したら退場!ですのでご注意くださいね。

最小公倍数を求めるときの考え方は最大公約数のときと同じです。
6と9の倍数を書き出してみましょう。とりあえず100以下まで。
- 6の倍数:6、12、18、24、30、36、42、48、54、60、66、72、78、84、90、96
- 9の倍数:9、18、27、36、45、54、63、72、81、90、99
よって公倍数は、18、36、54、72、90ですね。最小公倍数はこの中で一番小さいもの、18が正解です。
こうやって見ていくと、「最大公倍数」は数が無限になってしまうので無さそうです。「最小公約数」はどんな数の組み合わせでも1になります。
あんまり意味がないから習わないんでしょうね。。
最小公倍数はどんなときに使う?どんなことに使える?
たし算、ひき算、かけ算、わり算さえわかっていればお金の計算できるんだから、生きていくのに算数いらないじゃん!
よく聞きます。声に出さなくてもそう思っている子は多いかもしれません。
極端なことをいうと、確かにその通りです。
でも算数は論理的に物事を考えるためにとても大切なものです。
「最小公倍数」とか、高校で習う「微分・積分・いい気分」とか大人になって使うことはまずないけれども、考え方を育てるためにぜひがんばってほしいと思っています。
なので、日常生活でどう結びつけられるか、などは私も特に意識して記事を書くようにしています。
通分で必要
最小公倍数は、その後に習う分数の通分で使います。
よって、最小公倍数がわからないとその後で習う、分母の違う分数の足し算・引き算が出来ません。
例えば、
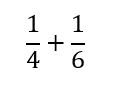
とか。
だから、歯を食いしばってがんばってください。

さっきと言っていることがちがうじゃん!!
その通り。これはただ事実を伝えただけです。
算数が苦手な理由の1つに、「前の単元が出来ないと今習っていることがわからない」があります。
「今やっとがんばろうと思ったのに、戻んなきゃいけないの??もうやだ!!」です。
でもこればかりは、やるしかありません。
富士山に登るのに、途中をすっとばしてヘリコプターで頂上へいくことはできません。
1合目登って、つぎ2合目、つぎ3合目です。
算数・数学が苦手な子には、前の単元に戻って教えることが多いですが、学校の先生は今の単元を教えるのに必死だし、休み時間になると職員室いっちゃうし、友達に聞くのはなんとなく恥ずかしいし、それで家庭教師はニーズがあるのかもしれません。
でも『フォートナイト』の建築だって、最初に階段とか壁を作る操作覚えて、それから組み合わせて上空に向かって矢倉を組んだりして、だんだんレベルを上げていくでしょ?
私に向かって「算数出来ない出来ない!」って言ってくるけど、みんなやろうと思えば出来るんだよ。
能力はあるけど、やりたくないだけ。
「通分で必要なんて味気ない!点数取るためだけの算数なのか!夢がない!」と思われそうなので、もう少し役立ちそうな例を次に挙げます。
お菓子を配るときに使える!
誕生日パーティの場面でお菓子を買うのでもいい、学校のグループ学習でもいい、何人かの子どもにあまりなく何かを配るときに最小公倍数は使えます。
1袋だとそもそも足りない。
2袋だと1個ずつみんなに配って6個あまる。何袋あればあまりなくなる?
そういうことってたまにあるでしょ?
1つ1つ計算していってもいいけど、12と9の最小公倍数を求める問題だってわかると、4袋買って1人あたり3個ずつ分ければぴったりだってわかります。
現実問題として、1人3個のチョコパイはぜいたくすぎるし、(3個も食べたら夕飯食えなくなる!)2袋で18個買って1個ずつ配って、残りはじゃんけん大会が王道かもしれません。
でも最小公倍数の考え方で3個分ければあまりない、ということを頭に入れておく。今回は出来なかったけど、余りが0になる状況がたまにやってきます。
そういう時にすぐ言えると、ちょっとかっこいいでしょ?
そんなことにも役立ちます。
約数をぬけもれなく書き出す方法
約数をぬけもれなく書き出す方法は学校で教えてくれると思います。復習で思い出してくださいね。
24の約数を書き出す場合。
まず1と24は絶対。

次に2で割る。24÷2=12。
2は約数だ、同時に12でも割れるということだから(24÷12=2)12も約数だ。

残りの約数は2と12の間にある。
24は3でわれるから3は約数だ(24÷3=8)。よって8も約数だ。

残りの約数は3と8の間にある。
4は約数だ(24÷4=6)。よって6も約数だ。

4と6の間は5しかない。でも24は5で割り切れないから約数ではない。
よって「1、2、3、4、6、8、12、24」が24の約数全てだ、と言えます。
約数は小さい側と大きい側をかけると24になるということもわかりますね。(1×24=2×12=3×8=4×6=24)
また、数直線で(上の図)で考えると、左側は混んでいるのに、右側の12と24の間は約数がないということもわかります。
最大公約数的な意見で、いい意見はあまりない
これは大人の世界でも子供の世界でもよくあることではないでしょうか?
そろそろ読むのも疲れてきたでしょ??
小学校、中学校でありがちな会話(女子と男子の対決)です。

A男:文化祭の出し物、チャーハンのフードファイト対決にしようぜ~!
B男:賛成賛成、それでいいじゃん。決めるの面倒くさいし。
C子:ちょっと男子~もう少し考えてくれない?他にもやりたいことある人いるでしょ?挙手お願いします!
D子:はい!劇団四季のようなミュージカルをやりたいと思います。
A男:それはつまんねーよ!誰が見に来るんだよ~!D子はD男が好きだからヒロインやりたいんだろ~!ヒュ~!
C子:ちょっとそんなこと言ったら、D子とD男が可愛そうじゃん!やめなよー!
D男:(C子よ、でかい声で繰り返さないでおくれ・・)はい、クレープ屋さんとかどうでしょう。毎年やってるし、、、
C子:クレープ屋さんいいわね、候補に入れておきましょう。他には?
C男:体育館全部仕切って暗闇の中でお化け屋敷やろうぜ!ぜったい楽しいって!
E子:C男、あんたなんか変なこと考えていないでしょうね!?
C男:変なことってなにそれ!E子キモすぎー!
A男:キモすぎー!(エコー)
E子:うるさい!うるさい!うるさい!あんたらほんっっと最低!
C子:はいはい、そろそろ多数決しましょうか・・。
結果、こうなっちゃうわけだ。
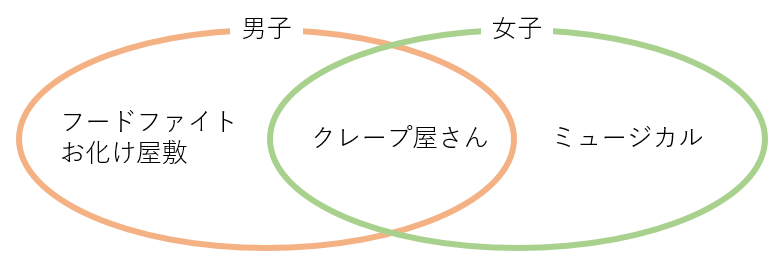
男子と女子でどちらもいいかなと思うのは「クレープ屋さん」。
これが最大公約数的な考え方です。
一番無難な結末になります。無難な結末は安定しているのですが、新しさ、ワクワク感が少し欠けます。やっぱり面白みがイマイチです。
大人はどうしても安定(最大公約数的意見)を求める、子ども若い人は失敗を顧みずにもっと思い切ったことを行う。
そこが若さの特権です。
最大公約数、最小公倍数とは?のまとめ
この記事では、
- 最大公約数、最小公倍数とは?~言葉の意味と求め方~
- 最小公倍数はどんなときに使う?どんなことに使える?
- 約数をぬけもれなく書き出す方法
- 最大公約数的な意見で、いい意見はあまりない
を解説しました。
気を張りすぎると疲れちゃうから、楽しくがんばってちょ!!








コメント