小学5年生算数で習う『割合』は、人によっては難問です。
私は家庭教師をしていますが、教え方でとてもつまずきました。
教え子が言うには、
- 文章題わけわかんない!
- 文章題は日本語だけど、意味わからないからよけい落ち込む
- 日本語わからない私は人間じゃない
- 人生オワタ…(もう算数やんない!)
大人からすると「いやいやおおげさなことを」と思いますが、子供からすると深刻な悩みです。
そこで『割合』の教え方を工夫してみました。
なんとかわかってもらえるようになりましたので、それをこれから紹介します。
小5算数『割合』の文章問題を手っ取り早く解く方法
『割合』の問題で、どんなところがわからないのかな?と聞いてみたところ、
まず、
- もとにする量
- 比べられる量
- 割合
が文章問題の中でどれなのかがわからない!というものでした。
でも、わからないところがわかる、大きな前進です。
では文章問題のどれが『もとにする量』なのか?言葉の配置で分かる方法を紹介します。
次の問題を見てみましょう。
「農園全体の面積が90m2で、野菜の面積が36m2です。野菜の面積は、農園全体の面積の何%ですか?」
この問題で『もとにする量』は「農園全体の面積」です。
なぜかというと次の法則があるからです。
この問題は、
『農園全体の面積の何%ですか?』
という文章なので、「何%(割合)」の直前である「農園全体の面積」が『もとにする量』です。
『割合』は30%とか、小数の0.3とか、分からなければ何%、で表されるのですぐに分かります。
残りの「野菜の面積」が『比べられる量』です。
もう一問、問題を見てみましょう。
「農園全体の面積は90m2です。農園全体の面積の40%が野菜の面積です。野菜の面積は何m2ですか?」
前の問題を少し変えて、野菜の面積を求める問題に変えてみました。
ここでもさきほどの法則を使うと
『農園全体の面積の40%が野菜の面積です。』
という文章ですから、40%(割合)の直前の「農園全体の面積」が『もとにする量』です。
「文章の言葉の配置で覚えるのならわかる」と子供からお墨付きをもらったので、とりあえずはこれで覚えると手っ取り早く問題が解けるのかなと思います。
以下、『割合』の理屈(割合はどんなことを計算しているのか?)について解説します。
小5算数『割合』の文章問題で省略されている言葉
国語、数学、理科、社会、英語。どの問題でも共通しますが、問題を解くときは、問題文をよく理解する必要があります。「割合」はほぼ文章問題なので、苦手な子がとても多いです。

問題文の意味がわからないと
- 問題文を読む気がおきない
- そもそも式とか答えとか、何もかけない
- (よって)や~めた
となってしまいます。
割合の文章問題ではつまずきやすいところがあります。それはある言葉が省略されて問題文が書かれているためです。
省略されている言葉とは「~を100%とすると」です。
もう一度、さきほどの問題を見てみましょう。
「農園全体の面積が90m2で、野菜の面積が36m2です。野菜の面積は、農園全体の面積の何%ですか?」
この問題文の前半
「農園全体の面積が90m2で、野菜の面積が36m2です。」
これはわかります。そのまんまです。
ところが、
「野菜の面積は、農園全体の面積の何%ですか?」
ここでとたんにわけワカメ(わけがわからん)になります。
この問題に「~を100%とすると」を追加してみましょう。
次のようになります。
「農園全体の面積が90m2で、野菜の面積が36m2です。野菜の面積は、農園全体の面積を100%とすると、何%ですか?」
さらに問題文を言いかえるとこうなります。
「農園全体の面積(90m2)を100%とすると、野菜の面積(36m2)は何%ですか?」
パーセントでなく、小数で言いかえるとこうなります。
「農園全体の面積(90m2)を1(=元)とすると、野菜の面積(36m2)は何%ですか?」
(この文章でも”1”と置いている農園全体の面積が『もとにする量』ということがわかります)
図にするとこのようになります。(図1)

図1.問題文を図に書くとこうなる
次に表にしてみましょう。(表1)
表1.問題文を表にするとこうなる
| 面積 | 割合 | |
| 農園全体の面積 | 90 m2 | 100%(=1) |
| 野菜の面積 | 36 m2 | ◯%(問題の答え) |
割合の問題は、文章を図や表に表すことが出来るととてもわかりやすくなります。
(わかりやすくなりました??)
もとにする量、比べられる量、割合
「割合わかんない!」といいながら、知らず知らずのうちに使っていたりします。
たとえば、
「私(わたし)10才、あなた40才。なら年れいは4倍違(ちが)うね。」

これは10才を『もと』にして、40才が何倍かを計算しています。
「私10才、あなた40才。なら年れいは400%違(ちが)うね」も同じ意味です。
ここでは10才が『もとにする量』です。「私」をもとにして、「あなた」は何倍かを計算しています。
「あなた」は「私」に比べられているので、40才は『比べられる量』です。
4倍(400%)が『割合』です。
もう一つ例を出します。
「私80点、あなた40点。あなたは私の半分ね!」
これも同じです。表2にそれぞれ何を表しているか示します。
表2.それぞれの数字は何を表している?
| 私の80点 | もとにする量 |
| あなたの40点 | 比べられる量 |
| 半分(=1/2=0.5=50%) | 割合 |
「私の80点を『もと』にすると、『比べられている』あなたの40点は、半分(50%)の『割合』ね!」
では、最初の問題にもどりましょう。
次のようになります。
「農園全体の面積が90m2で、野菜の面積が36m2です。野菜の面積は、農園全体の面積(=100%とすると)の何%ですか?」
農園全体の面積90m2を100%としています。これ(農園全体の面積90m2)がもとにする量です。
元にする量を30でも90でもなく100%にするのは、それがきりのいい数字でわかりやすいからです。
この問題では、野菜の面積の割合は36 ÷ 90 =0.4=40%です。
もう少し正確に書くと、
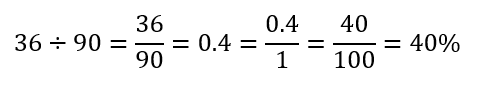
これはどういう意味かといいますと、農園全体を100%とした場合、野菜の面積は40%ということ。または農園全体を1とした場合、野菜の面積は0.4ということ。
「90m2と36m2」を比べるより「100%と40%」を比べた方がわかりやすいですよね。
また、100%と40%で比べると、元にする量はつねに100%だから100%を省略(しょうりゃく)できて40%だけ使えばいいじゃん!となります。
棒(ぼう)グラフを図2に示します。よくわからんと言っているあれです。
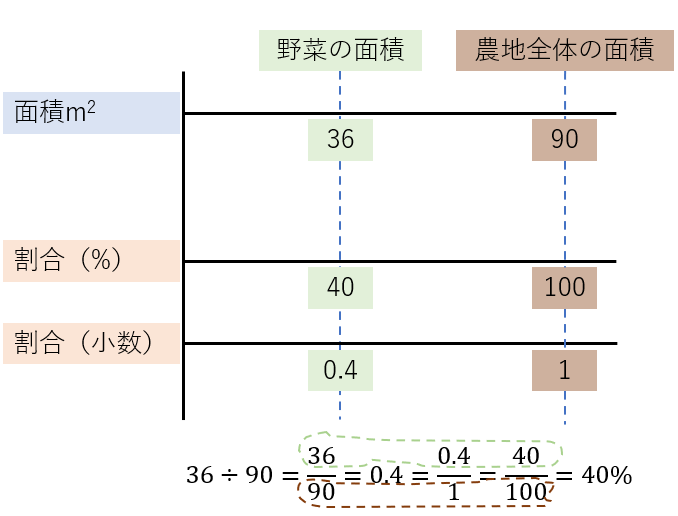
図2.棒(ぼう)グラフにするとこうなる
グラフと式の数字はちゃんと対応(たいおう)していますね。
小5算数『割合』の計算3パターン
割合の計算では3つのパターンがあります
- 割合を計算する
- 比べられる量を計算する
- もとにする量を計算する
それぞれ見てみましょう。
A)割合を計算する
式は、
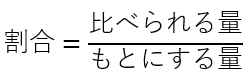
割合を求めるときは、『もとにする量』が分母です。
上の農園の問題の例では、
.png)
ですね。
B)比べられる量を計算する
このとき、わかっているのは『もとにする量』と『割合』ですから、次の式になります。
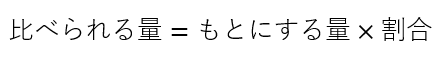
「なぜ×(かける)になるのか?」と言う質問がありました。
割合というのは「もとにする量の何倍なのか?」ということを計算するために使います。
10才と40才の年れいの例では、
10才(もとにする量)の4倍(割合)が40才(比べられる量)です。
「農園全体の面積90m2の40%はいくつか?」という問題があったら、
「農園全体の面積90m2を元にして、その40%はいくつか?」ということで、
言いかえると「農園全体の面積90m2を元にして、その40%(=0.4倍)はいくつか?」という質問と同じ意味です。
「倍」だから「×(かける)」です。
C.もとにする量を計算する
3つ目の計算方法はこちらです。
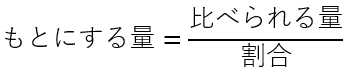
おそらくこれが1番難(むずか)しいと思います。式をがんばって覚えてください。
小学校で今ここをどう教えているかは、残念ながら私は知りません。
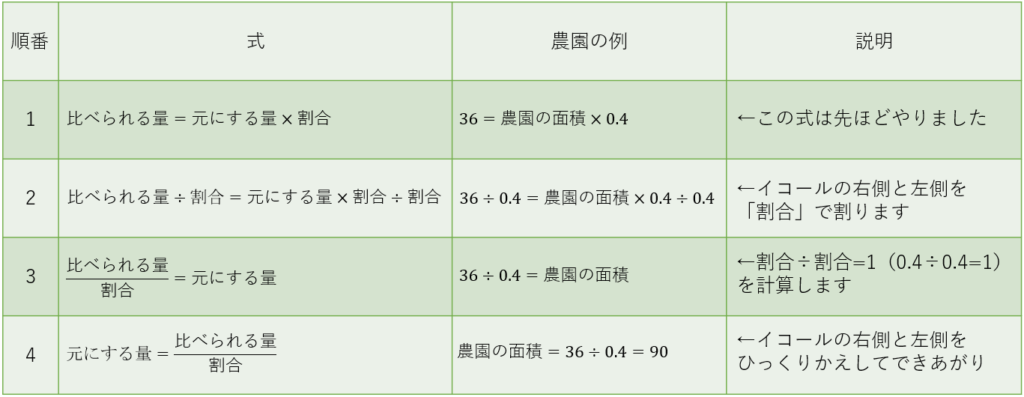
なぜこうなるかの式変形は中学で習います。(表3)楽しみにしていてくださいね。
表3.もとにする量の計算式が「比べられる量÷割合」である理由
4.おまけ(勉強のポイント)
今回、算数で「割合(わりあい)」を習いました。
これに関連して、勉強をするうえでとても大事なことは、
- もとにする量を「昨日の自分」
- 比べられる量を「今日の自分」
にすることです。
これは、「昨日の自分」に対して「今日の自分」は何%がんばったか?ということです。
式にすると、こうなります。

そうするとがんばれるし、つらさが減ります。
なぜかというと、分母も分子も自分だから割合をコントロールしやすいからです。自分ががんばった分だけよくなります。
反対に、悪いことすると一気にだだ下がりしますが。。

(一歩を確実に上がるのが大事)
ほとんどの人は、
- 元にする量を「他人」
- 比べられる量を「自分」
にしています。
式にすると、
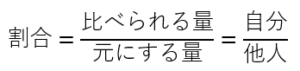

(周りの目が気になるのは仕方ないことですが・・)
他人はコントロールできませんから割合(%)を上げるのは大変です。足の引っ張り合いもよくないですしね。
また、他人と比較(ひかく)すると疲れてしまいます。
「(私は)Aさんよりはすごい?」「Bさんよりできない?」「Cさんと比較するとみじめになる」「Dさんになら勝てる」・・・。もうきりがありません。。
あーだこーだ心のなかでウジウジ思いながら、無駄な時間だけが過ぎていきます。
ライバルはいたほうが頑張れます。だけど同じ方向を向いて競うのよ。それ忘れたらただのケンカだからね!
クラスの誰々さんに勝ったら入試合格!なんて基準の学校はこの世に存在しません。
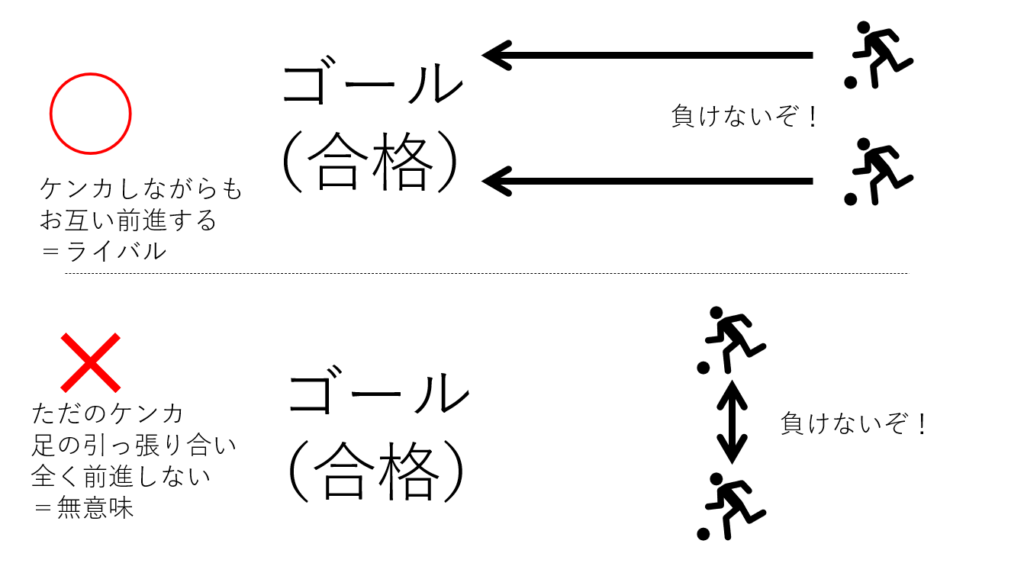
勉強(特に受験)の心構えとして極めて大事です。一歩一歩がんばっていきましょう!
「小5算数『割合』の文章問題を手っ取り早く解く方法」のまとめ
この記事では、
- 『割合』の文章問題を手っ取り早く解く方法
- 『割合』の文章問題で省略されている言葉
- もとにする量、比べられる量、割合
- 『割合』の計算3パターン
- おまけ(勉強のポイント)
について紹介しました。
かなり昔ですが『おぼっちゃまくん』というアニメがあって、その歌詞で
「1日1分!3日で3分!つ~らか~と~ば~い」というものがあります。
昨日よりも今日は1%よくなるように心がけてください。そうすると、計算では365日後には365日前の37.4倍になっています。(もちろんやりたくない日もありますが)
継続は力なりですね。










コメント