【小学5年生の算数】体積の求め方を解説！体積の換算表とお風呂プリンの計算も

私が小学生の時、体積の求め方は「たて×よこ×高さ」ですぐわかりましたが、単位が変わったときがとても苦労しました。

「1m³は何cm³ですか？」という問題が出て、正解した子が数人いました。

わからない子は正解した子の所へノートを持っていって◯、✕をつけてもらうことになったのですが、

私は授業が終わるまで正解できず、大きな✕を何回も書かれて撃沈げきちんした記憶きおくがあります。

おかっぱ頭くらいの女の子だったかな、これでもかというくらい大きなペケ（✕）を赤えんぴつで何度も何度もつけられたので、今でも覚えています。

恨うらみでもあったのかな～と当時は思ったのですが、今思うとただ任務に忠実ちゅうじつだっただけのような気がします。

よって、単位の換算かんざんも記事に載のせました。

最後に、ただ計算、計算ではおもしろくないので、風呂ふろいっぱいにプリンを作ったらどれくらいの材料が必要かも計算してみました。

こういうのを想像しながら計算すると算数もなかなかおもしろいなと感じることが出来ると思います。

空想科学読本、的な。。

 

立法体と直方体とは？

立方体（りっぽうたい）と直方体（ちょくほうたい）とはどんなものかおさらいしてみましょう。

まず両方とも「方」の漢字が入っています。

「方」は四角形を表す漢字です。

社会で「前方後円墳（ぜんぽうこうえんふん）」という言葉を習いましたか？

これは「前は四角、後ろは円のお墓」という意味です。

 

立方体はサイコロがイメージしやすいです。

たて、よこ、高さが全部同じ長さで、辺と辺の角度がすべて90°の立体ですね。

直方体は、辺と辺の角度がすべて90°は同じですが、たて、よこ、高さの長さが違ちがうものを直方体と言います。

1. たて、よこ、高さが全部違う長さ→直方体
2. たて、よこが同じ、高さだけ違う→直方体
3. たて、高さが同じ、よこだけ違う→直方体
4. よこ、高さが同じ、たてだけ違う→直方体
5. たて、よこ、高さが全部同じ長さ→立方体

 

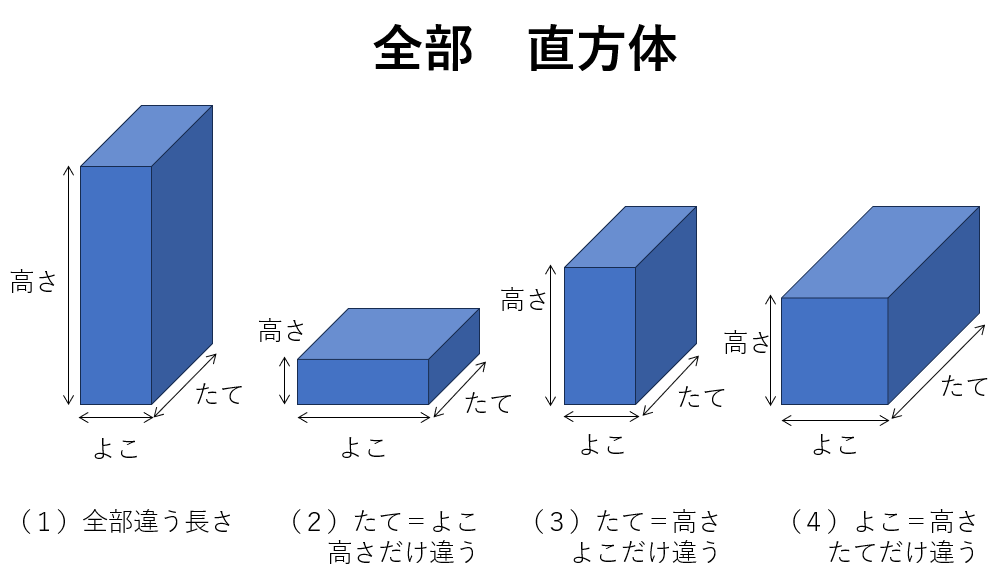
立方体と直方体の体積の求め方

直方体の体積は、たて×よこ×高さで求まります。

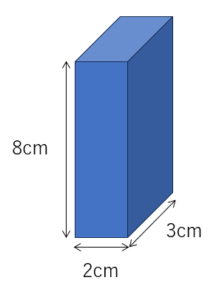
この直方体の体積を求めてみましょう。

計算式は3(cm)×2(cm)×8(cm)で

答えは3×2×8=48cm³です。

48cm³は48立方センチメートルと読みます。

cm³の3は長さを3コ（たて、よこ、高さ）かけたことを表しています。

面積だとcm²だから長さを2コかけていますね。（たて×よこなので）

ですから、単位をみれば「長さ」なのか「面積」なのか「体積」なのか一目でわかります。

• m、cm、mm：長さ
• m²、cm²、mm²：面積
• m³、cm³、mm³：体積

という具合です。

立方体の体積も、たて×よこ×高さで求まりますが、全部同じ長さなので、一辺×一辺×一辺とも表現できます。

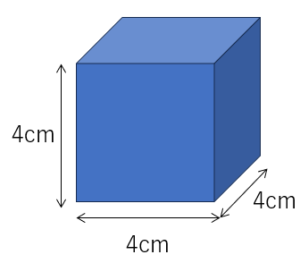
計算式は4(cm)×4(cm)×4(cm)で

答えは4×4×4=64cm³です。

 

体積の単位の換算

さてここからがお待ちかね、単位の換算かんざんです。

私の（過去の）トラウマ領域りょういきです。暗さの演出のため灰色はいいろにしました。

最初、私は「1m³は100cm³じゃん！だって1m=100cmだから！」と答えました。で、思いっきりバツを食らいました。

さてどこがおかしいのでしょうか？図で考えるとわかりやすいです。

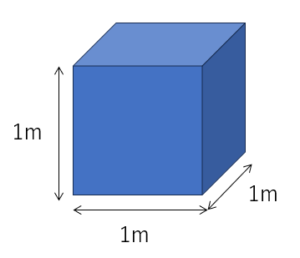
この図で体積を計算すると、

1(m)×1(m)×1(m)=1m³です。

1m=100cmです。これを図に書き足してみましょう。

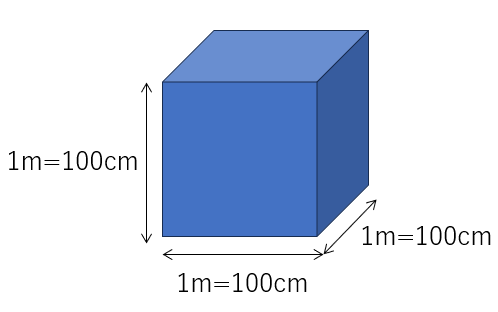
単位をcm（センチ）で計算すると、計算式は

100(cm)×100(cm)×100(cm)となるわけです。

私の言い分、「1m³は100cm³じゃん！だって1m=100cmだから！」の「だって1m=100cmだから！」は合っていました。でもそれを3回かけ算しなければいけなかった、そこが間違いでした。

100(cm)×100(cm)×100(cm)=1000000cm³です。すなわち百万立方センチメートルです。

3回かけるからいきなり数字が大きくなるのですね。そこがちょっと気をつけないといけないところ。

単位の換算ですが、よく使うのはこれらでしょうか？

• 1m=100cm
• 1m³=100cm×100cm×100cm=1000000cm³
• 1l（リットル）=10cm×10cm×10cm=1000cm³〔リットルは体積を表す単位です〕
• 1l（リットル）=10dl（デシリットル）〔デシは10分の1という意味があります〕
• 1ml（ミリリットル）=1cm³
• 1000ml（ミリリットル）=1l（リットル）〔ミリは1000分の1という意味があります〕
• 1cc（シーシー）=1cm³〔お料理で出てきますね）

 

体積の求め方の応用～お風呂プリンの計算～

「たて×よこ×高さ」

はっきり言ってこれだけだと何にも面白くないんですよ。

算数の醍醐味だいごみはテストでいい点を取ることではないのです！

体積の求め方と単位の換算がわかると、いろんな空想が出来ます。世界が広がるのです。（大げさじゃないよ）

身近な例は何がある？

これ↓は、子どもの夢の10位以内に入るものではないでしょうか？

バケツプリンじゃ実際に売ってるから面白くない。（あとバケツは丸いから「たて×よこ×高さ」の計算ができないという大人の事情もあります）

お風呂にプリンをしきつめよう。

実際にはやりません。

紙とえんぴつと体積の計算で、空想するだけ。

本当にやったら嫁おかかにボコボコにされます。お風呂にダイブする可能性もなくはないですが・・。

 

さて、プリンのレシピを見てみましょう。

ぷるぷる食感！ 基本のプリンのレシピ動画・作り方 | DELISH KITCHEN

【2018年11月レシピリニューアル】 子供にも大人にも大人気な「プリン」 今回は蒸し器なしでも作れるレシピのご紹介です！ カラメルのほのかな苦味とプリンの濃厚な甘さが絶妙♪

delishkitchen.tv

ここを参考にしました。

表に必要な材料とその量を示します。この材料でプリンが600cc出来ます。

600ccということは、600cm³ですね。

表１．材料（150ccを4カップ分＝600cc）

牛乳ぎゅうにゅう	400cc
卵たまご	2コ
砂糖さとう	80g
カラメルソース
砂糖	60g
水	大さじ1(=15cc)
湯	大さじ1(=15cc)

 

さて、うちのお風呂の大きさはどれくらいでしょうか？

定規で測ってみました。もちろん写真は載のせられません。

おおよそですが、たて100cm、よこ60cm、高さ50cmでした。

お風呂の体積はいくつでしょうか？先ほどの式を思い出して下さい。

たて×よこ×高さ＝100(cm)×60(cm)×50(cm)=300000cm³（三十万立方センチメートル）です。

表１の材料でプリンが600cm³出来ます。

お風呂は300000cm³です。

600cm³のプリンが何個あれば300000cm³になるでしょうか？

計算式は300000(cm³)÷600(cm³)=500

そうです。600cm³のプリンが500コあれば、お風呂をプリンでいっぱいにすることが出来ます。

ということは表１の500倍の材料が必要ということになります。

全部500倍して表2に書き直してみましょう。

表２．お風呂をプリンでいっぱいにするために必要な材料

牛乳	200000cc
卵	1000コ
砂糖	40000g
カラメルソース
砂糖	30000g
水	7500cc
湯	7500cc

ゼロがいっぱいあって、なかなか大変な数字になってきましたね。

これだけだと、へぇすごい数だなぁ、、で終わってしまいます。

近くのスーパーのチラシを確認してみました。

表３．スーパーのチラシによる材料の値段

牛乳1l（リットル）	238円
卵10コ	118円
砂糖500g	195円

 

お風呂をプリンでいっぱいにするためにはお金はどれくらい必要？という問題を計算してみましょう。

こういう問題の方が、私はわくわくするし、計算してて楽しいです。

牛乳の値段

必要な牛乳ぎゅうにゅうの体積（容積）は200000ccです。

1cc=1cm³ですから、

200000cc=200000cm³ですね。

牛乳は1l（リットル）で238円です。

1l（リットル）＝1000cm³ですから、1000cm³で238円です。

200000cm³の中に1000cm³は何個あるでしょうか？

計算は、200000÷1000=200

よって1000cm³が200本必要ですから、238円×200=47600円かかる計算になります。

 

卵の値段

同じやり方で卵たまごも計算してみましょう。

必要な卵の個数は1000コです。

卵は10コで118円です。

1000コの中に10コはいくつあるでしょうか？

計算は、1000÷10=100

よって10コパックが100必要ですから、118円×100=11800円かかる計算になります。

 

砂糖の値段

砂糖さとうも同様に。

必要な砂糖は40000+30000=70000gです。

砂糖は500gで195円です。

70000gの中に500gはいくつあるでしょうか？

計算は、70000÷500=140

よって500gの砂糖が140袋ふくろ必要ですから、195円×140=27300円かかる計算になります。

 

ここまでの計算でおわかりだと思いますが、

 

水とお湯は水道水と電気ポットでかんべんしてもらうとして、

全部でおいくらでしょうか？

表４．お風呂をプリンでいっぱいにするために必要なお金

牛乳1l（リットル）200本	47600円
卵10コを100パック	11800円
砂糖500gを140袋	27300円
合計金額	86700円

合計87600円となりました。

「うーん1000円くらいだったら少しはやる気が出るけど、8万円はちょっと厳きびしいなぁ。」ということが、スーパーにダッシュする前にわかるわけです。

仮にがんばってお風呂プリンを作ったとします。

このプリンのカロリーは247kcal（キロカロリー）。一日の摂取せっしゅカロリーがだいたい2000kcalなので、そこから計算すると、お風呂の中で2ヶ月くらいプリンを食べ続けて生きることが出来ます。

まぁ30分しないうちにあきるけどね。

2ヶ月後のプリンってそもそも腐くさってるしね。

そういう意味で1人で食べるのはよろしくないです。

今回の場合、2000コのプリンが出来るから、1人2つ食べても1000人に分けられます。

それはそれで大変な作業であることが予想されます。

ここまでわかると、食材も無駄むだになるし、あんまりやりたくないですよね。

こんなことが紙とえんぴつで計算して想像できるのが算数です。

実際にお金は使ってないけど、計算していろいろ想像して、私はだいぶ楽しめました。

 

こういう計算が積み重なって、電球が発明された、宇宙うちゅうへロケットが飛び出すことが出来るようになった、電話（スマホ）が開発された、そんな例は数えればキリがありません。

 

↓お父さんに頼んだら、買ってくれるかも！？

 

【小学5年生の算数】体積の求め方を解説！のまとめ

この記事では、

• 立法体と直方体とは？
• 立方体と直方体の体積の求め方
• 体積の単位の換算
• 体積の求め方の応用～お風呂プリンの計算～

について紹介しょうかいしました。

算数キライな子でも「出来ると楽しい」と言います。

出来ないからキライなのかもしれません。

そうすると出来るように頑張がんばるしかないのですが、楽しく頑張れたら理解は早くなるかなと思います。

私ができることといえば、楽しく頑張れるような記事を今後も書いていくこと、なのでヘンテコなこと書くかもしれませんが、どうぞお付き合い下さい。。

P.S.　先日作ったプリンです。コツはいかにレシピに忠実に作るかですね。