将棋駒はなぜあんなにも綺麗なのでしょうか?昔は長方形の駒だったようですが、今は五角形の形をしていますね。その五角形の角度を測定し、理想の角度との比較も行ったので紹介します。
測定の方法ですが、駒の角度をノギスの寸法測定と三角関数tan(タンジェント)の計算から求めました。
測定の結果から、測定した将棋駒の角度は「理想の角度」に対して誤差5%以内ということがわかりました。

分度器使わなかったの?

使えなかったの。やってみればわかるわよ。
将棋駒の角度を求めるための材料と方法
将棋駒の角度ですが、
- 以前測定した駒の寸法
- 角度を計算するtan(タンジェント)
を用いて求めることにします。(分度器を使わなかった理由は後述)
駒の寸法
駒の寸法はこちらの記事で紹介しています。

上の記事と重複しますが、寸法を測定した場所は第1図の
- 辺CD
- 辺AH
- 辺BE
- 辺GH
です。

第1図
この情報があると、駒の角度が分かります。
例えば第2図の右下の角度(∠BCI)を知りたい場合、三角形BCIで考えると、2辺(赤線)は測定結果からわかり、2辺の情報がわかるとtanを用いて角度が計算できるという具合です。
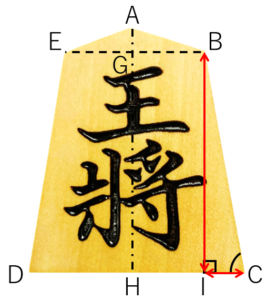
第2図
tan(タンジェント)は高校の数学で習いますが、難しい場合は飛ばしてくださいね。
分度器を使わなかった理由
分度器を使った方が早いのでは?という意見もありそうなので分度器を使わなかった理由を最初に説明します。
分度器の大きさって使ったことある人はだいたいイメージできますよね。手のひらよりちょっと小さいくらい。対して将棋の駒は親指よりちょっと大きいくらい。
将棋の駒が小さすぎて目盛を(たぶん)当てられないんですよ…
分度器が家になかったのでインターネットか文具店で購入しようとしましたが止めました。そのようなわけで駒の寸法とtan(タンジェント)から求めてみようと思いました。

実験もお料理も一緒。全体をイメージしてからGo!がおすすめ。

にんじんの皮はいつもむき忘れてるけどね…。
この駒の例のように対象物が小さすぎるとか、狭いところに測定したいものがあって分度器が入らないとか、直接角度を測定できない場面もありますので、別の測定方法も知っておくと便利です。
角度を計算するtan(タンジェント)の説明
「三角形は2辺と1つの角度が決まると形が決まる」中学校の数学の図形の証明で習うところです。tan(タンジェント)はこれを応用しています。

舞桂ねえちゃん、ねむい…

難しかったら読み飛ばしてね。
直角三角形で、辺aと辺bの長さが決まると、角度の1つは90°ですので三角形の形が決まります。(第3図)さらに言うと直角三角形の辺aと辺bの比が決まると、その比の三角形は全て相似形になります。
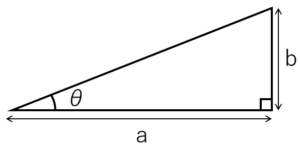
第3図
それはすなわち、辺aと辺bの比が決まると、∠θの値が1つに決まることを意味しています。
それならば、辺a、辺bの比と角度θの関係をあらかじめ調べて一覧表にしておけば、全ての直角三角形において、辺a、辺bの長ささえ測ってしまえば角θが計算出来てしまいます。
その一覧表が詰まった計算式がtan(タンジェント)です。
公式は
です。
一覧表にしてみると表1のようになります。
表1.辺a、辺bの比と∠θの関係
| 番号 | 辺a | 辺b(=b/a) | ∠θ[°] |
| 1 | 1.00 | 5.67 | 80 |
| 2 | 1.00 | 2.75 | 70 |
| 3 | 1.00 | 1.73 | 60 |
| 4 | 1.00 | 1.19 | 50 |
| 5 | 1.00 | 1.00 | 45 |
| 6 | 1.00 | 0.84 | 40 |
| 7 | 1.00 | 0.58 | 30 |
| 8 | 1.00 | 0.36 | 20 |
| 9 | 1.00 | 0.18 | 10 |
比に着目しているので辺a、辺bの単位は不要です。
番号3は三角定規の60°、番号5は三角定規(直角二等辺三角形)の45°、番号7は三角定規の30°です。
例えば、
- tan45°=1
- tan60°=√3
になりますね。

起きなさーい!

すぴぴー。はっ!
将棋駒の角度の計算結果
王(玉)、飛車、角、金、銀、桂馬、香車、歩の8種類の駒に対して、角度を求めてみました。第4図に示す、θ1、θ2、θ3です。
θは「しーた」と読み、角度を表すギリシャ文字です(xやyと同じ)。後ろに数字を付けて、θの子分1、θの子分2、θの子分3という具合に名前をつけています。

ちなみに猫の口みたいな「ω」は「オメガ」と読みます。
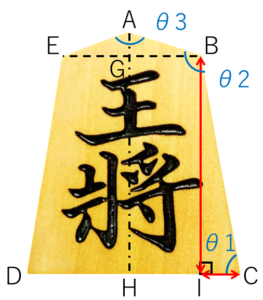
第4図
角度θ1の結果
第4図の∠θ1を求める場合、辺CI、辺BIの情報があれば計算ができます。
表2.∠θ1の計算
| 駒 | 辺CI[mm] | 辺BI[mm] | ∠θ1[°] |
| 王将(玉将) | 4.6 | 28.4 | 80.7 |
| 飛車・角 | 4.0 | 26.7 | 81.4 |
| 金・銀 | 3.7 | 25.1 | 81.5 |
| 桂馬・香車 | 3.7 | 24.6 | 81.5 |
| 歩 | 3.5 | 23.3 | 81.5 |
結果、∠θ1=80~82°となりました。
角度θ2の結果

第4図(再掲)
∠θ2は3つの角度の合計になります。
∠ABGは辺BG、辺AGの情報があれば計算可能ですね。
表3.∠θ2の計算(単位:長さはmm、角度は°)
| 駒 | 辺BG | 辺AG | ∠ABG | ∠CBI | ∠ABC |
| 王将(玉将) | 9.5 | 3.7 | 21.0 | 9.3 | 120.2 |
| 飛車・角 | 9.0 | 3.4 | 20.7 | 8.6 | 119.3 |
| 金・銀 | 8.8 | 3.4 | 21.1 | 8.5 | 119.5 |
| 桂馬・香車 | 7.9 | 3.1 | 21.4 | 8.5 | 119.8 |
| 歩 | 7.1 | 2.8 | 21.7 | 8.5 | 120.2 |
結果、∠θ2=119~120°となりました。
角度θ3の結果

第4図(再掲)
∠θ3は二等辺三角形ABEで考えると、
で求まりますね。
表4.∠θ3の計算
| 駒 | ∠θ3[°] |
| 王将(玉将) | 138.1 |
| 飛車・角 | 138.6 |
| 金・銀 | 137.9 |
| 桂馬・香車 | 137.3 |
| 歩 | 136.6 |
結果、∠θ3=136~139°となりました。
理想の角度との比較
駒には理想の角度があるそうです。
理想の角度を真値として、測定値の相対誤差を求めてみました。(表5~7)
相対誤差[%]=|真値ー測定値|/真値×100 で計算しますので、0%に近いほうが理想の角度に近いことになります。
表5.∠θ1の相対誤差
| 真値[°] | 測定値[°] | 相対誤差[%] | |
| 王将(玉将) | 81 | 80.7 | 0.3 |
| 飛車・角 | 81.4 | 0.5 | |
| 金・銀 | 81.5 | 0.7 | |
| 桂馬・香車 | 81.5 | 0.7 | |
| 歩 | 81.5 | 0.6 |
表6.∠θ2の相対誤差
| 真値[°] | 測定値[°] | 相対誤差[%] | |
| 王将(玉将) | 117 | 120.2 | 2.8 |
| 飛車・角 | 119.3 | 2.0 | |
| 金・銀 | 119.5 | 2.2 | |
| 桂馬・香車 | 119.8 | 2.4 | |
| 歩 | 120.2 | 2.8 |
表7.∠θ3の相対誤差
| 真値[°] | 測定値[°] | 相対誤差[%] | |
| 王将(玉将) | 144 | 138.1 | 4.1 |
| 飛車・角 | 138.6 | 3.8 | |
| 金・銀 | 137.9 | 4.3 | |
| 桂馬・香車 | 137.3 | 4.7 | |
| 歩 | 136.6 | 5.1 |
この結果から、測定した将棋の駒の角度は理想の角度からおよそ5%以内であることがわかりました。
また、理想の角度の駒を使うと、20枚を一周並べるときれいな円形になるようで、第5図は実際に並べてみた写真です。

第5図
これは∠θ1=81°が関係しています。角度がぴったり∠θ1=81°なら、1枚の駒の傾斜は (90-81)×2=18° になり、駒が20枚そろうと18°×20=360°となり、ちょうど円周の角度と一致するためです。
また、駒の大きさが違うもので一周並べた場合、並べる順番にちょっとした工夫が必要です。
小さい順から並べたりすると、最後つながらなくなる場合があります。よかったら考えてみてくださいね。
角度はなぜθ(シータ)なのか?
角度はなぜθ(シータ)という記号が使われるのでしょうか?
これはインターネットで調べた情報ですが、レオンハルト・オイラーという人がθという記号を使用したのが最初と言われています。
オイラーは18世紀の数学者で、片目を失明していました。晩年両目を失明しますが、それでも数学の研究に没頭していたようです。
膨大な数の論文を残したことでも有名です。
まさに天才です。
「天才が最初に角度をθと表記した、だからみんなθを使おうぜ!」
そういうことなのかもしれません。
オイラーは幾何学でも多大な功績を残しました。幾何とは簡単に言うと図形のことです。
『容疑者Xの献身』という映画にも”幾何”という言葉が出てきました。
登場人物の石神という数学者のセリフ
”幾何と見せかけて実は関数の問題”
です。

(見方を変えると、見えないものが見えてくるのじゃ)
例えばこんな問題です。
一見、四角形が出てくるので図形(幾何)のように見えますが、実は関数で答えが出ます。
この四角形は底面がx軸に接し、左上・右上の点はy=x^2の関数上に位置しています。図示すると下のようになりますね。
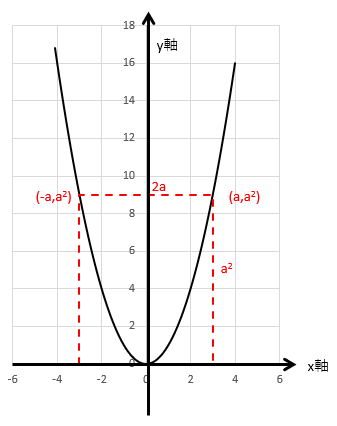
4辺の長さの合計が16なので、2a+a^2+2a+a^2=16の方程式を解けば答えが導き出せます。
でも、関数で図示すると「答えは1つに決まる」ということが直感的にわかるので、関数で考えられることも大事なことです。
答えは、a^2+2a=8 → (a+4) (a-2)=0 → a=-4、2 → aは0より大きいからa=2、面積は4×4=16 です。
将棋駒の角度の測定結果まとめ
この記事では、
- 寸法測定とtan(タンジェント)から将棋の駒の角度を計算
- 理想の角度と測定結果の比較
を行いました。

将棋もいいけど、ちゃんと学校の勉強もやるのよ。

ぶーぶー。

今夜は肉なしカレーね💢

勉強がんばるぞー。おー!
・関連記事はこちら








三角形を用いた重心の求め方-1-120x68.png)

コメント