前回の記事では、将棋の駒の大きさを測定し、比較しました。

そのときのグラフがこちらです。
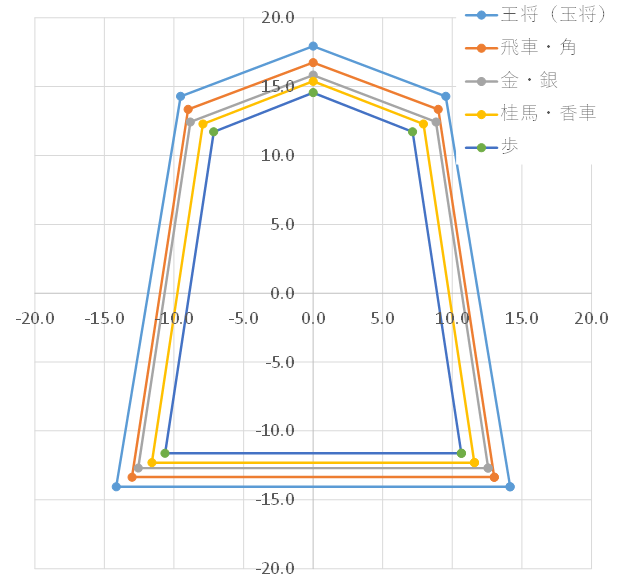
このグラフを描いたときに、駒の重心位置を求めましたが、その重心の求め方を記載します。
将棋というよりも数学の記事ですが、興味のある方はどうぞご一読ください。
重心の求め方
重心とは、将棋盤で説明しますと、将棋盤を指1本でバランスがとれて支えることができる点です。
将棋盤は長方形なので、対角線の交点が重心になります。
仮に将棋盤が平面の四角形だとして、頂点に同じ重さのおもりをぶらさげたときに釣り合う点でもあります。(第1図)
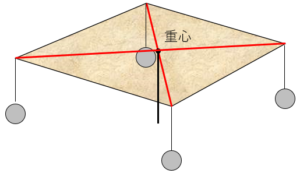
第1図
三角形の重心は、3つの頂点の座標の平均値です。(第2図)
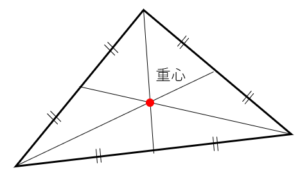
第2図.三角形の重心
これを応用して駒(五角形)の重心を求めます。
五角形は3つの三角形に分割でき、まずそれぞれの三角形の重心を求めます。
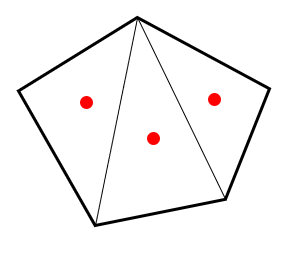
第3図.五角形を三角形に分割
そして3つの重心を頂点とする三角形を考えると、その三角形の重心が五角形の重心になります。(第4図)
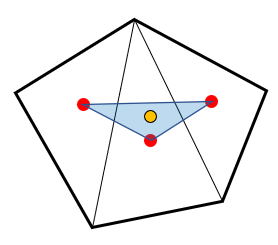
第4図.五角形の重心
ただし1つ注意点があります。分割された三角形の面積が同じなら頂点の座標の平均値を単純にとればいいのですが、面積が違う場合は重みづけをする必要があります。
たとえば、三角形の面積の比が1:1:2の場合は、25%、25%、50%という具合に座標に重みづけをします。
三角形のそれぞれの重心の座標がA、B、Cとすると、
重心の座標=0.25×A+0.25×B+0.5×Cといった具合です。
※A、B、Cにx,yそれぞれ当てはめて計算します。
駒の重心を求めてみる
王将駒の重心を求めてみましょう。
三角形に分割する仕方は何通りかありますが、どれでも結果は同じになります。
面積が求めやすいので点線で切ってみます。(第5図)
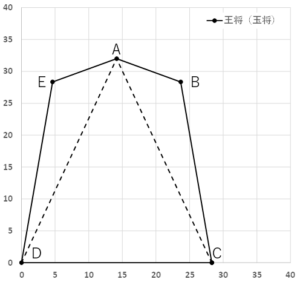
第5図.駒の分割
△ABC、△ACD、△ADEの重心をそれぞれP、Q、Rとすると、三角形の面積と重心の座標は次のようになります。
表1.三角形の面積
| 三角形 | 面積[mm2] | 割合 |
| △ABC | 127 | 0.18 |
| △ACD | 453 | 0.64 |
| △ADE | 127 | 0.18 |
| 合計 | 706 | 1 |
表2.重心座標
| 頂点 | x座標[mm2] | y座標[mm2] |
| P | 22.0 | 20.1 |
| Q | 14.2 | 10.7 |
| R | 6.3 | 20.1 |
よって駒(五角形)の重心座標は、
x座標=22.0×0.18+14.2×0.64+6.3×0.18=14.2[mm]
y座標=20.1×0.18+10.7×0.64+20.1×0.18=14.1[mm]
となります。
図示すると第6図のようになります。
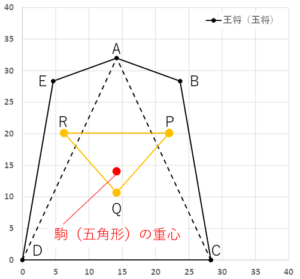
第6図.駒(五角形)の重心
五角形と黄色い三角形の重心がずれているように感じるのは重みづけのためです。
その他の重心の求め方
他の重心の求め方を紹介します。
計算などは行わず、測定して求める方法です。
駒の角に糸をつけ、ぶら下げます。
第7図は、駒の左上の角に糸を付けてぶら下げています。

第7図
その角を通る垂線を引きます。糸におもりを付けて鉛直下向きにし、その角を通るように糸を配置します。
別の角で同じことを行い、2つの線の交わったところが重心です。
駒は左右対称なので、線対称となる線が2つ目の線で大丈夫です。
第6図と第7図を重ね合わせてみました。(第8図)
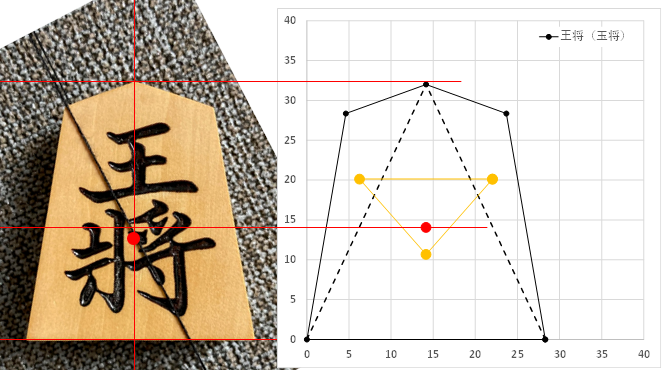
第8図
糸で測定した方が、やや下の方に重心があります。
駒は上側と下側で厚みが違うので、その影響が出たためと考えられます。
まとめ
この記事では、
- 重心の求め方2つ
- 王将駒の重心位置の計算
について解説しました。
頭の体操という意味合いで読んでいただけたら幸いです。
次は駒の角度にフォーカスしていきたいと思います。






三角形を用いた重心の求め方-1.png)


コメント