
うちの子、算数の文章問題が本当に苦手なのよね~。何かコツとか無いのかしら…。

問題を見た瞬間に頭が真っ白になって、答案用紙も真っ白!な~んて。
算数の文章問題が苦手なお子さんは結構いるようです。お母さんお父さんは悩んでいて、子供さんは案外ケロっとしているんですよね。。今回は算数の文章問題に関する記事です。
算数の文章問題が苦手な理由ですが、主に3つだと私は考えています。(1つ目の理由に気づいたとき、私は驚きました)
〔算数の文章問題が苦手な理由〕
- 問題文を読まないで解答しようとしている
- 解くための基本公式を忘れてしまっている
- 計算ミス(筆算のかけ算、わり算など)
なぜこの3つかというと、3つのステップをクリアすることによって解答にたどり着くからです。
また、私は現役で家庭教師をしていますが、実際に教えていてそういうお子さんを見かけるからです。
この記事を読むと、算数の文章問題が解けない理由、解くためのコツ(3つの理由の対策方法)がわかります。わが子でも文章問題が解けるようになると思います。
特に理由の1番に焦点を当てて、なるべく実例と図を使って解説するようにしました。
気になる方はぜひ読んでみてください。
算数の文章問題が解けない理由
最初に算数の文章問題が解けない理由3つの解説、次に算数の文章問題を解くためのコツを紹介します。
最後にお子さんが算数を嫌いにならないためのマルの付け方について書きますので参考にしてください。
算数の文章問題が解けない理由3つを再度挙げます。
- 問題文を読まないで解答しようとしている
- 解くための基本公式を忘れてしまっている
- 計算ミス(筆算のかけ算、わり算など)
2番目の「基本公式」については復習して勉強し直せば大丈夫です。
解くための基本公式で苦手な子が多いのは、5年生で習う『割合』です。割合についてはこちらの記事を参考にしていただければと思います。
3番目の「計算ミス」も計算問題を繰り返し解いたり、筆算の方法を再確認したりすればミスは減っていきます。
筆算で特に間違いやすいのは小数の割り算です。小数点の位置をどこにすればよいか忘れがちです。
それについてはこちらの記事を御覧ください。
よってここでは、1番目の理由『問題文を読まないで解答しようとしている』に焦点を当てて、実例を交えて見ていきます。
~~~
先日、家庭教師で勉強を教えているときにこんなことがありました。
次の文章問題を解いてみることにしましたが、子どもがわからなかったので解説をしました。
たて18cm、よこ12cmの折り紙を全部同じ大きさの正方形に紙が余らないように切り分けたい。一番大きな正方形に切り分けたとき、正方形の1辺の長さは何cmになりますか?
12の約数:1、2、3、4、6、12
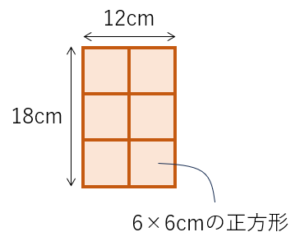
たて6cm、よこ9cmの紙をタテヨコにしきつめて正方形を作りたい。一番小さい正方形の1辺の長さは何cmになりますか?
6・・1、2、3、6
9・・1、3、9
答え3cm(・・正解は18cm)
理由1の「問題文を読まないで解答しようとしている」です。
計算ドリルの一番上には「最小公倍数」「速さ」「割合」などテーマが大きく書かれてあります。そして、文章問題に出てくる情報(数字)は必要最小限です。
ですから文章問題をしっかり読まなくても「今は『速さ』の単元だから、この数字とこの数字を割り算すればいいじゃん!」でなんとなく解けてしまいます。でもそれは本当に解けたとは言えません。
道のりと速さの単位が違っていてもそのまま割り算してしまうので、当然間違えてしまいます。
子どもと色々お話してみたら、
「文章問題に出てきた数字をとりあえずかけたり割ったりすれば答えは出てくるかなぁと・・」
「文章問題ざっくり読んで計算してた」
やっとゲロってくれました。(笑)
国語の文章はちゃんと読めるし、問題も解ける子です。でも算数になると『問題文を読まないで解答しようとしている』のが癖になってしまいているようです。
原因がわかったというのは大きな前進です。文章問題読んでないのなら、ちゃんと読めばいいでしょ!
ちなみに問題2を図に描くとこうなります。(図2)

図2.問題2の図式化
算数の文章問題を解くためのコツ
算数の文章問題を解くためのコツはこちらです。
- まず算数の文章問題を最初から最後までゆっくり音読して読みましょう。
- つぎに問題を解くのに必要な「わかっていること」には直線、求めるものには波線を引きましょう。
- 図形などに置き換えられるものは図にしてみましょう。
1番目は算数の文章問題だけでなく、日常生活でもとても大切です。相手の話を最後まで聞いてから答えないと、会話があさっての方向へ飛んでいってしまいます。
社会人では特に大事。相手の会話をしっかり聞いて、会話の流れにそった返しが出来るだけで仕事のやりやすさが全然違います。そういう訓練でもあります。だから大人になっても非常に役立つスキルです。
2番目は実際に線を引いてみましょう。

求めたいものは「正方形の1辺の長さ(波線)」です。
棒線には説明しやすくするため①②③と番号をつけています。
〔棒線①『たて18cm、よこ12cmの折り紙』〕
まず、『たて18cm、よこ12cmの折り紙』を問題用紙の白いところに書いてみましょう。
本当に18cm、12cmの大きさを定規で測って書く必要はありません。イメージをしたいだけなので、縦長の長方形を手書きで書けばOK。
寸法もちゃんと入れておきましょう。(図3)
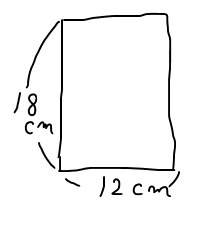
図3.たて18cm、よこ12cmの折り紙の図
〔棒線②『全部同じ大きさの正方形に紙が余らないように切り分けたい』〕
次に『全部同じ大きさの正方形に紙が余らないように切り分けたい』と書いてあるので、パッと思いつく正方形でイメージしてみましょう。タテヨコ1cmの正方形なら出来そうですね。また、18と12が2で割り切れる数なのでタテヨコ2cmの正方形もできそうです。
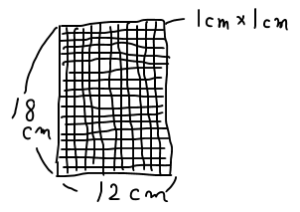
図4.1cm×1cmで切り分けた場合
でも5cmの正方形は、18と12は5で割り切れないからダメだなぁ。問題文にも『紙が余らないように切り分けたい』と釘が刺されています。
〔棒線③『一番大きな正方形』〕
棒線①②までの問題文だったら、答えはいくつかあります。1cmも2cmもそうだし、おそらく3cmも正解です。
棒線③の『一番大きな正方形』と書いてあるのを見て、答えは1つだけだなと気づきます。
また、18と12の両方で割り切れる数じゃないと正方形って作れないな、とわかれば答えは出たも同然です。
正方形の1辺の長さは18や12よりも絶対に小さくなりますから(紙を切るんですから)、答えは1~12cmの間のどれかです。
1つ1つ試していけば、答えは6cmと出てきます。
もちろん最大公約数の問題だとわかれば、18と12の約数を書き出して、共通する一番大きな数(=6)が答えです。
18の約数:1、2、3、6、18
12の約数:1、2、3、4、6、12
よって答えは6cm。
一文一文、一行一行、ていねいに文章を読んでいけば、答えに必ずたどり着けます。
逆に言えば、答えに必ずたどり着けるような問題文を算数の先生は作っている、とも言えます。
算数の文章問題のマルの付け方(補足)
算数の文章問題を解くうえで、3つの大切なことを解説しました。
おわかりの通り、文章問題は下の図5の過程を経てようやくマルがもらえます。
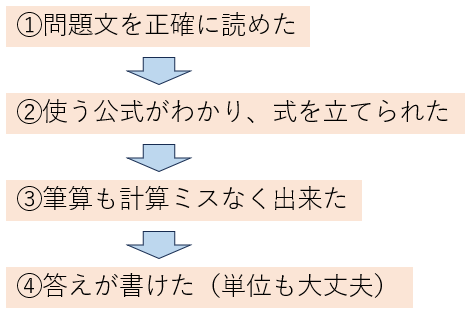
図5.マルがもらえるまでの過程
4段階クリアしてようやく正解がもらえるのですから、なかなか大変です。
もし答えが正解していなければ、①②がクリアできていてもバツ。①すらできていなくても同じバツ。0点です。
頑張って解いたのにバツをもらうと、やる気がなくなっていきます。バツが続けば続くほどもうやだ!と気持ちが折れてしまいます。
このようにマルの付け方を改善したらどうでしょうか?
①②はちゃんとできていた→マル
③で間違えた→バツ
よって答えを間違えた→バツ
こうすると、途中までマルだったんだということがわかります。そしてどこで間違えたのかがわかります。どこで間違えたのかがわかると、そこを直せば正解できるんだということがわかります。
ただ答えがバツだけだと、ぼんやりなんとなく間違えた、何がいけないのかもわからない。よってどこを直せばいいのかもわかりません。そうすると、よくわからん数学は苦手、キライ、私は算数ができない人間なのだ、、とアキラメモードになってしまいます。
ですから、丸をつける中で「間違えた原因はここ、そこを直せば出来るようになるよ」というメッセージが伝わると、解いている本人も「じゃ、もうちょっと頑張ろう」という気持ちになるのではないでしょうか?
算数の文章問題のコツ!文章問題が解けない原因と対策を実例をまじえて解説のまとめ
この記事では、
- 算数の文章問題が解けない理由
- 算数の文章問題を解くためのコツ
- 算数の文章問題のマルの付け方(補足)
について解説しました。
算数もわかると楽しいことありますし、大人になって役立つことたくさんありますから、ぜひあきらめずに頑張ってください。算数や数学やっても意味ないよって言う人たまにいるけど、そんなことありません。
苦労した分だけ、自分にいいことが返ってきますよ。










コメント