将棋の駒は8種類ありますが、その寸法をノギスで測定し、大きさを比較してみました。
測定の結果、中心の縦の長さで寸法を比較すると、
- 王・玉=32.0[mm]
- 飛車・角=30.1[mm]
- 金・銀=28.5[mm]
- 桂馬・香車=27.7[mm]
- 歩=26.2[mm]
となりました。

同じ種類の駒でも微妙に大きさが違ったよ。

七色のグラフも作ったので見てちょうだいね!
また、その測定結果を用いて、駒の体積の公式を求めてみました。
駒の体積をV[mm3]、縦、横、厚みなどの6つの寸法をa、b、c、d、e、f[mm]とすると、
\(V=\frac {1}{6}\{3e(ad+bc)-bc(e-f)-\frac {d}{b}(ad+bc)(e-f)\}\)
で表せることがわかりました。

うへ、文字だらけだ。

将棋だって符号の羅列じゃない。おんなじよ!

(こわーい)
将棋駒の大きさの測定位置
測定した将棋の駒の情報を表1に示します。
表1.将棋駒の情報
| 購入先 | 前川榧碁盤店 |
| 種類 | 彫駒 |
| 字体 | 菱湖(りょうこ)※1 |
| 材料 | 黄楊(つげ)※2 |
※1菱湖(りょうこ):将棋の駒の書体の1つ、巻菱湖とも言われる
※2黄楊(つげ):将棋の駒の材料としてよく用いられる低木
こちらが将棋駒の写真です。歩は予備1枚含めて19枚あります。(第1図)

第1図.将棋駒の写真
測定した駒は、王(玉)、飛車、角、金、銀、桂馬、香車、歩の8種類です。
測定位置を第2図に示します。駒の頂点をA、B、C、D、Eとし、点Aから辺CDにおろした垂線との交点をH、辺AHと辺BEの交点をGとします。

第2図
このとき、
- 辺CD
- 辺AH
- 辺BE
- 辺GH
- 辺CD側の厚み
- 点A側の厚み
を測定しました。駒は左右線対称であると仮定しています。測定器具はノギスを用いました。

たくさん手を動かしたから目をつぶっても測れるよ!

これだけ測ったら当面忘れないわね…。
将棋駒の大きさの測定結果
測定結果を表2に示します。「飛車と角」、「金と銀」はほぼ同じ大きさのようですね。
表2.測定結果(単位:mm)
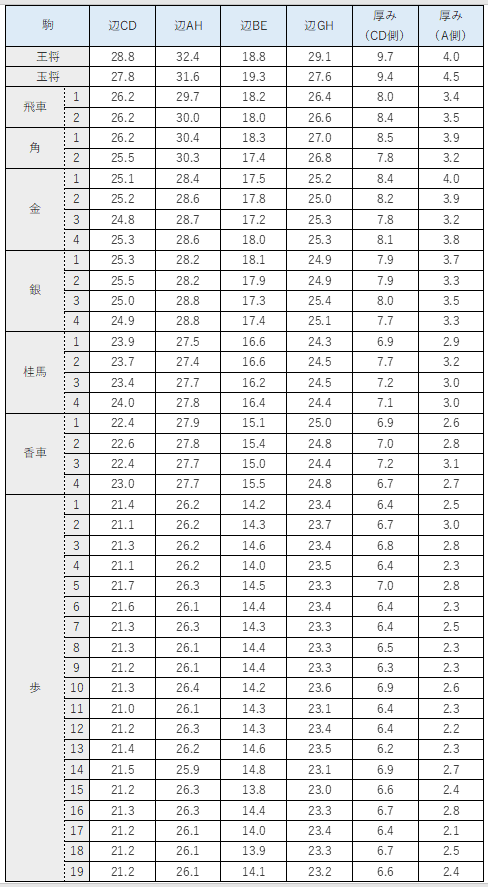
表だけだとわかりにくいので、グラフで比較してみましょう。駒は1種類につき複数枚あるので、同じ大きさの駒は平均値を取ります。第3図のグラフがその結果です。
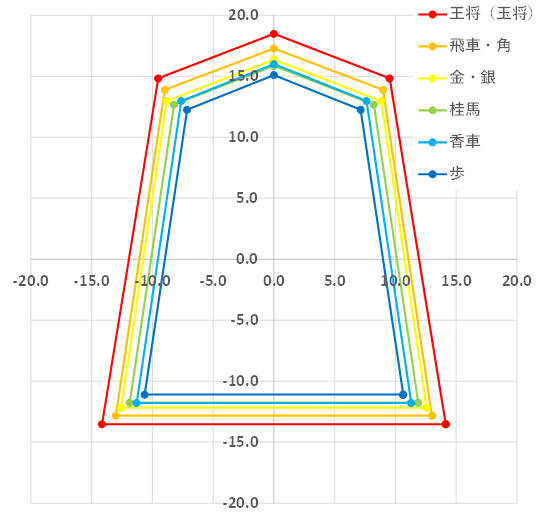
第3図.駒の大きさの比較(単位:mm)
グラフを見ると等間隔の割合で面積が変化していそうです。また相似の五角形みたいですね。
面積も計算してみました。第4図がその結果ですが、約1.1倍ずつ変化していることがわかります。
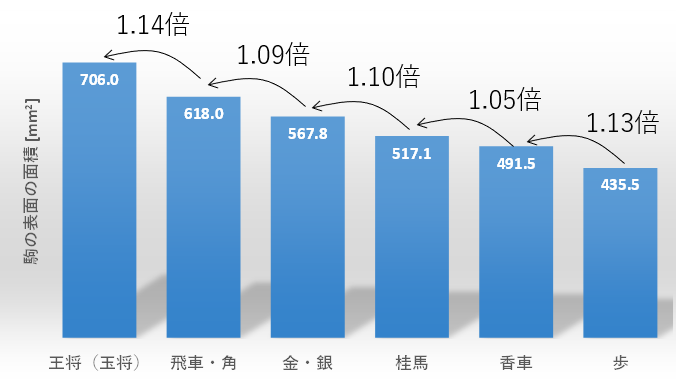
第4図.駒の面積の大きさの比較

表よりもグラフのほうがわかりやすいね。

パッと見てわかる方が伝わりやすいわね。
次に、これらのデータを用いて、将棋の駒の体積を求めてみましょう。
将棋駒の体積を計算する方針
最初に「今持っているデータ」とその材料を「どう使って体積を求めていくか」について記載します。理由は、方針をしっかり立てておくと後戻りしなくて済むためです。
今持っているデータ
これまで将棋駒の寸法と角度を求めましたが、寸法がわかれば将棋駒の体積を求めることが出来そうです。
測定した寸法(a、b、c、d、e、f)を第5図に示します。
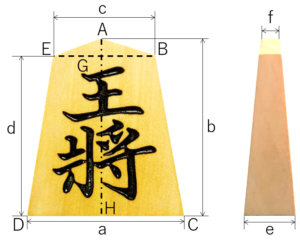
第5図
体積を求める方針
体積の求め方ですが、計算できる形に駒を分割してそれぞれの体積を求める方法を取ります。

バラバラにして最後に合体!だね。
分割の方法ですが、まず第6図の赤線で分割し、2つの立体にします。

第6図
第6図の赤線の上側の立体をさらに分割すると、三角柱が1つと四角すいが2つになります。(第7図)

第7図
第6図の赤線よりも下側の立体を切り出したのが第8図。頭が寒そうですね。

第8図
上向きに立体を延長します。(第9図)

第9図
第9図を正面から見た図形が第10図ですが、赤線で切断すると四角柱と四角すいになります。
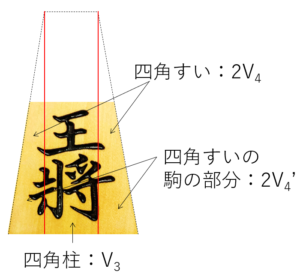
第10図
V3は四角柱なので立体の体積の公式で計算可能、V4‘の体積は四角錐の体積を求める公式と立体の相似の考え方を用いれば体積が求まります。
これで方針が決まりました。

計算問題も山登りと一緒。方向決めてからGo!がおすすめ。

方向間違えると引き返すの大変だしね。
四角錐の計算公式と立体の相似
駒の体積を求めるために必要な2つの公式を確認します。
四角錐の体積を求める公式
四角錐の体積は、「底面×高さ÷3」で求めることが出来ます。
第7図で底面の縦・横の長さをa、b、高さをhとすると四角すいの体積Vは次式です。
\(V=\frac {1}{3}abh\)
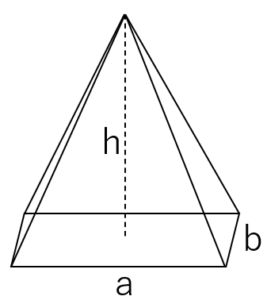
第11図
立体の相似
三角錐も四角錐も円錐も、底面と平行に立体を切れば、切った立体は相似になります。
2つの立体が相似である場合、第8図の例では「赤い四角錐」と「透明な四角錐(赤い四角錐も含む)」ですが、辺の比がa:bならば、体積の比はa3:b3になります。
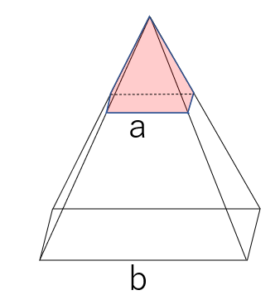
第12図
ちなみに平面の場合は、縦と横で計算しますから、比はa2:b2ですね。
将棋駒の体積の公式を求めてみた
計算の方針は決めたので、あとは必要な寸法を求めて地道に計算していきましょう。
数字を直接当てはめて計算してもいいのですが、文字のままで計算すると体積を文字式で表すことができます。体積を文字式で表すと、数字を代入すれば体積が出てくるので、あとでとても楽です。
公(一般的)に使える式だから公式と言われます。
途中の計算過程はとてもしんどい内容だったので省略しますが、一部はこんな感じです。(第13図)項が多すぎて計算ミスの修正にめちゃくちゃ時間がかかりました。

第13図
結果、それぞれの体積は次のような式で表せました。
\(V_{1}=\frac {1}{2}cf(b-d)\)
\(2V_{2}=\frac {c}{3b}(b^{2}e-2bde+d^{2}e+bdf-d^{2}f-b^{2}f+bdf)\)
\(V_{3}=\frac {1}{2b(e-f)}(2be-de+df)(bce-abe+ade-adf)\)
\(2V_{4}’=\frac {(ab-bc)(3b^{2}e^{2}-3bde^{2}+3bdef+d^{2}e^{2}-2d^{2}ef+d^{2}f^{2})}{3b^{2}(e-f)}\)
整理するとこのようになります。
\(V=V_{1}+2V_{2}+V_{3}+2V_{4}’\)
\(V=\frac {1}{6}\{3e(ad+bc)-bc(e-f)-\frac {d}{b}(ad+bc)(e-f)\}\)
項がどんどん消去されていって、ここまで簡単になったのでちょっと嬉しかったです。
この式を用いて駒の体積を求めてみましょう。王将駒の各寸法a,b,c,d,e,fを式に代入すると、V=5205[mm3]となりました。(一応CADで駒の図形を描き、ぴったり5205[mm3]となることを確認しています)
将棋の駒の大きさと駒の体積の公式のまとめ
この記事では、将棋の駒の大きさの測定結果と、それを用いて将棋駒の体積の公式を求めてみました。
また、四角すいの体積の公式・立体の相似についても説明しました。

ただの計算問題より、こっちの方がちょっと面白かった。

具体的な問題だとイメージがわくわね。
算数や数学の問題で
- 太郎さんが◯km先まで行くのに、途中まで自転車で移動して、その後歩きました。歩き出した地点は何km先でしょうか?
という問題を見かけます。大勢の人が見るので致し方ないのかもしれませんが、もし次のような問題だったらどうでしょうか?
- 彼女とケンカしたイケメン俳優が自宅のお母さんの元へ自転車で泣きながらダッシュしました。ところが途中でパンクしてトボトボ歩いて帰りました。歩き出した地点は何kmでしょうか?」
計算過程と結果は同じになるでしょうが、私は後者の方がストーリーがあって面白いです。皆さんはどう思われますか?
・関連記事です










三角形を用いた重心の求め方-1-120x68.png)
コメント